Библиотека CMSIS DSP. Так ли быстр целочисленный квадратный корень?
Небольшое сравнение функции вычисления квадратного корня из библиотеки CMSIS DSP и моей реализации.

Как-то долго я не обращал внимания на эту библиотеку, но вот насталов время.
Там есть куча всяких полезностей, в том числе и быстрых математических функций. И даже вычисление целочисленного квадратного корня. Круто, я смогу отказаться от самописной реализации в пользу той, которую предлагает компания ARM.
Для начала проверим, так ли быстр армовский квадратный корень и подходит ли он именно для тех задач, для которые необходимы мне.
Функция из бибилиотеки DSP имеет два варианта, это 16 бит и 32 бита, флоат версию рассматривать не будем. Моя реализация только версию для 32 бита (на момент начала эксперимента)
С моей версией можно ознакомиться здесь, или же пройти по ссылке на мой пак для Keil'а на gitlab (В разделе "Полезные ссылки")
О CMSIS DSP можно почитать в папке с установленным Keil, у меня это
C:/Keil_v5/ARM/PACK/ARM/CMSIS/5.4.0/CMSIS/Documentation/DSP/html/index.htmlПриступим к тестам.
Код для тестирования максимально прост, в качестве подопытного выступает Миландр 1986ВЕ92У на частоте 8 МГц.
В текстовом виде код не буду прикладывать, во время теста я не думал о написании этой заметки, а общался с товарищем в WhatsApp, вот и слал туда эти картинки.
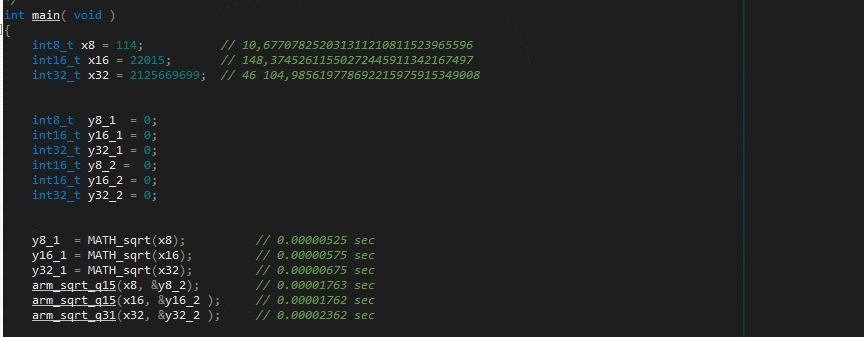
Что мы видим? Три вида переменных x8, x16, x32 - это те числа корни которых нужно найти, я заранее посчитал их на калькуляторе и написал в комментариях.
Далее объявляем пеменные в которых будут результаты, с суфиксом _1 мои, с _2 - ARM. Они объявлены сразу, что бы и мои, и ARM функции были в одинаковых условиях.
Следующие 6 строк это вычисления. Комментарии - время выполнения каждой строчки.
Вот и результаты выполнения кода...
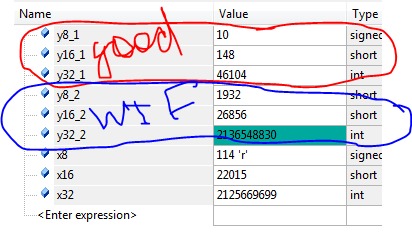
Что такое???
Тут нужно оговорится и сказать, переданные и полученые значения CMSIS DSP необходимо интерпретировать несколько по другому (в отличии от моих):
...input value. The range of the input value is [0 +1) or 0x0000 to 0x7FFF.Входной аргумент это не просто целое число, а 32768 доля от единицы. Это значит, что in = 1000, это не что иное как 1000/32768.
В итоге имеем весьма быстрое вычисление всеми функциями. Хороший результат. А теперь подробнее об алгоритме работы.
И CMSIS DSP и мой вариант используют один и тот же метод нахождения результата, за одним исключением - это первое приближение к результату.
Вот вариант CMSIS DSP
x0 = in/2 [initial guess]
x1 = 1/2 * ( x0 + in / x0) [each iteration]У меня же немного более хитрый вариант.
А терь посмотрим как можно ускорить мой вариант (код открыт, почему бы не попробовать)
Самым слабым местом является многократное повторение одного и того же кода:
ax = (d + value / d) >> 1;
d = (ax + value / ax) >> 1;
ax = (d + value / d) >> 1;
value = (ax + value / ax) >> 1;Применительно к моему коду столько строк актуально для 32 разрядов, а у нас ещё 16 и 8 есть. Нужно лишь удалить несколько строк и готово. И теперь результаты будут следующими:
- 16 бит - 0.00000475 сек, что на 0.00000100 сек быстрее моей 32 битной версии
- 8 бит - 0.00000350 сек, что в 1,6 раза (на 0.00000175 сек) быстрее моей 32 битной версии
Неплохое достижение.
Но мои функции могут работать только на ядрах Cortex M3 и старше, тогда как библиотека CMSIS DSP может быть использована и на M0. Наверняка вы знаете почему так - нет?
За более детальное знакомство с функцией из CMSIS DSP спасибо некому Shura Luberetsky, который в комментарии ткнул в грубой форме (за что коммент был удален) меня носом в описание функции. Если чесно, то спасибо ему, заставил меня вернуться к данной теме и почитать документацию более детально, поскольку я совсем её забросил.
На этом всё. Хорошего кодинга.